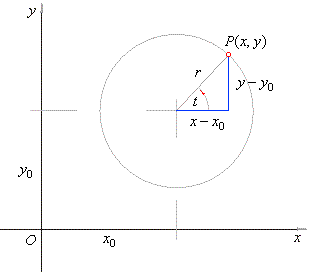Lesson 13 Conservation of Energy

It is impossible not to conserve energy because energy is always conserved. This is a fundamental principle of physics. There are three parts to the Law of Conservation of Energy including: energy, momentum, and angular momentum. What is energy? Energy is observed in many shapes and forms on earth and the universe. However, if energy is always conserved how do objects get started?

W = Fh
Weight = Force x Height

If the object is near earth then W = mgh due to the force of gravity.

Therefore U = mgh or potential energy is equivalent to the "work put into it," where potential energy depends on vertical distance. Take an inclined plane for example:

The potential energy of the object depends on the height of the inclined plane. In a system with two adjacent inclined planes without any other external forces exerted on the object, the object would travel down the inclined plane where potential energy would change into kinetic energy, and then change into potential energy as it reaches the same initial height on the second inclined plane.

dW = Fdx

W = integral (Fdx)

If work is done against a constant opposing force, as in lifting a block from one height to another then:
                    h1
W = F x integral (dx)
                    h0
              h1
     = Fx |
              h0

   = Fh1 - Fh0

U = Fh

W = U1 - U2

The work is the difference between the potential energy at the two heights or the change in potential energy.

If work is done with no opposing force, then the force is still work integrated over disance where:
              x1
W = integral (Fdx)
              x0

however the result of the work is to accelerate the block, therefore it gains speed. If the interval is considered in terms of speed:

W = integral (madx)  F = ma

W = integral (m (dv/dt) dx)

     = integral (m (dx/dt) dv)

     = integral (mvdv)
                   v1
W = m (integral (v) dv)
                   v0
                          v1
     = m 1/2 v^2 |
                          v0
                   2             2
W = 1/2 m v  - 1/2 m v
                  1              0
Therefore work is the change in the quantity k = 1/2 m v^2 or kinetic energy, the energy of motion.

Potential energy changes constantly while kinetic energy is constantly in flux. When the sum of both is considered, the totality of energy is a constant:

E = U + K

energy = potential energy + kinetic energy

            = constant

The transfer of potential and kinetic energy can be observed in the following video:



 James Joule is credited with the discovery of the conservation of energy by studying how much mechanical energy turns into heat as a large weight is lifted to a certain height. This has a precise potential energy:

U = mgh

Joule arranged to have falling weights turn paddle wheels in an insulated container of water. Joules then measured the water's temperature, given the loss of potential energy always turns into precisely the same amount of heat because loss is also gain in energy. Vibrations of atoms have a number of effects by jostling air that creates soundwaves, and generates heat. Heat spreads from molecule to molecule dispersing energy but not destoying it. Energy is neither created or destroyed. Heat dispersion is merely spread into vibrations that increases potential and kinetic energy of atoms by exactly the amount that has been lost. Activity can be measured in the form of the same basic unit known as a Newton meter or 1J.

4.2 J = 1 cal, the standard measure of heat.

Energy flows throughout the universe ever changing but constant, and is not lost but transformed into heat. As energy changes forms, it becomes harder and harder to retrieve at the atomic level.

The following video explains the conservation of energy further:

Lesson 12 The Millikan Experiment

All the forces and quantities of matter can be divided into their individual parts. For example the photon (light), the phonon (sound), the proton (matter), and electricity (electron) are all example of individual units. J.J. Thompson was born in 1856 and lived until 1940. Thompsonn was not only an English pysicist, but also a Nobel laureate who created the mass spectrometer and discovered the electron and the existence of isotopes. However, Thompson is heavily associated with his use of the Cathode Ray Tube experiment to discover the electron. A cathode ray tube is a vacuum tube with electrodes on each side. An electrical current is sent through the vacuum tube creating a "ray" that can be deflected by both a magnet and and electrical field. Thompson realized that the experiment could not be conducted because the tube contained traces of gas left by the glass-blower. Thompson then heated the tubes, which allowed the traces of gas to leave the tube. Once the vacuum was achieved, Thompson's used a magnet/electrical field to study the deflection of the "ray." From this, Thompson concluded that the "ray" was composed of a negatively charged particle, the electron, and the experiment was successful.  Below is an animation of a cathode ray tube:


After the electron was discovered, Millikan would be the physicist to measure the charge of an electron using oil, an iron pot, and electrical power. However, during this time period there was a strong influence from Europe, regarding advances in the sciences. These advances fueled Millikan's ambition and included: Nobel Prize winner and Univeristy of Chicago professor Albert Michelson's creation of the instrument to measure distances by the interference of light waves; William Ramsay's discovery of the elements helium, xenon, krypton, and neon; William Rontgen's discovery of x-rays; Guglielmo Marconi's adaption of the wireless telegraph; Marie Curie nobel prizes form her work in physics and chemistry; Albert Einstein's Theory of Relativity; work by Max Planck and Johannes Stark; and J.J Thompson and A.J. Wilson's discovery of the effects of x-ray radiation and the cloud chamber method for measuring charge. With all these advances at the frontier of physics, Millikan was determined to use his skills with precise measurments in order to push the frontier slightly farther.

Therefore, Millikan performed the famous Oil-Drop experiment. Millikan first ionized a gaseous cloud, and utilized both x-rays and radium. Millikan then used a powerful electrical field to balance the force of gravity and suspend the cloud of water without motion. However, this presented a problem because the water cloud would evaporate. Therefore, Millikan used oil droplets that would not disappear in order to detect the effect of an electron. Millikan theorized that if an electrical field is applied to an electrically charged oil falling through the air, then the resulting charge of the electron could be determined using F=ma:

ma = summation (F)

F(gravity) = mg and viscosity

F(viscosity) = 6(pi)Rnv
where R = the radius of the sphere, n = the viscosity of the air, and v = velocity.

F(viscosity) is a constant speed, however the velocity grows until viscosity balances gravity.

v = mg/ 6(pi)Rn

Below is a video showing the principle of viscosity:


Millikan then needed to measure the speed in order to find out how big each drop of oil was because they were to small to see with the human eye:

D(density) = m/(4/3)(pi)R^3                                      mg/6(pi)Rn = v
R^2D = m/(4/3)(pi)R                                                 m/(pi)R = 6nv/g
(4/3)R^2D = m/(pi)R

(4/3)R^2D = 6nv/g
R = sqrt (6nv/(4/3)gp)

The electric field creates an electric force so F(electricity) = electric fields strength times the strength on the oil drop. F(e) = qe because the force of electricty will be an integer multiple of the fundamental unit of electricity.. The electric field will drive the drop up until a constant speed is reached.

qE - mg = 6(pi)Rnv

v = qe - mg/6(pi)Rn

v (electric field on) = qe - mg/6(pi)Rn                   v (electric field off) = mg/6(pi)Rn

v(on) + v(off) = qe/6(pi)Rn

qe = (v(on) +v(off)) 6(pi)Rn

q = (v(on) +v(off)) 6(pi)Rn/e

Millikan took meticulous steps in order to ensure that his experiment yielded the correct result. Millikan minimized the turbulence of the droplets between the two plates by housing the plates in iron pots. The air was filtered through glass wool and an atomizer was used to spray the finest mist of oil droplets into the chamber. Light was filtered out by a solution of copper sulfate that coated a one meter tube of wate to eliminate the heat of water. Below is a video displaying actual footage of Millikan's experiment repeated:



Millikan found that the charge of an electron was 4.77 x 10^-10 or 1.602 x 10^-19 coulombs, a two percent difference from the prior experiment performed by Thompson. In 1923, Millikan was the first native born American to get the Nobel Peace Prize in physics.

Lesson 11 Gravity, Electricity, and Magnetism

Three values govern the nature of the world. These values include: the force of gravity, the speed of light, and the electric charge of an electron. The Gravitational constant (G) is equivalent to 6.7 x 10^-8 dyne cm^2/g^2, a value so small that scientists do not have the appropriate technology to measure the force exactly. The speed of light (c) is equivalent to 3 x 10^10 cm/sec, and serves as a tool to measure the vastness of space. In other words, distance in space is measured by light-years or the distance light travels in one year. The electric charge of an electron (e) is equivalent to 4.7 x 10^-10 esu. These values were not discovered outright by a single physicist or scientist. Instead, numerous physicists contributed to these findings:

In 1675, Ole Romer observed the delay of the eclipse of Jupiter's satelites in order to calculate the velocity of light.

In 1849, Hippolyte Fizeau used rotating wheels to measure the speed of light through air and water.

In 1850, Jean Foucault named and improved the gyroscope and discovered the speed of light with a series of rotating mirrors.

In 1926, Albert Michelson measured the time it took light to travel from two large peaks (Wilson/San Antonio) in Los Angeles. Michelson found that it took .0001 sec for light to travel from one peak to the other. These peaks were roughly 30 km apart. Therefore speed is equal to distance/time, and the speed of light is about 3 x 10 ^8 m/s. Below is a video displaying how the speed of light can be measured using a chocolate bar and a microwave:

Another distinct force is magnestism:

F(m) = k(m) p1p2r^
                         r^2

Magnetic poles, represented by p1 and p2, are always in pairs that are equal and opposite. This equation is strikingly similar to the equation of the force of electricity. In 1820, Hans Christian Oersted discovered this relationship between electricty and magnetism known as electromagnetism. Oersted found that a compass needle would deflect from magnetic north when an electric current from a battery was switched on and off. Oersted first believed that magnetic effects were produce from all sides of the wire, but after future investigation, he discovered that an electric current produces a circular magnetic field as it flows through a wire. Below is an example of his experiment:



Gravity:
G = 6.7 x 10^-11 Nm^2/kg^2

Electricity:
K(e) = 9 x 10^9 Nm^2/e^2 (coulombs)

Magnetism:
K(m) = 1 x 10^-7 Ns^2/e^2 (amperes or coulombs per second)

Due to the relationship of electromagnestism, James Clark Maxwell discovered that magnestism and electricty were not independent:

K(e)/K(m) = 9 x 10^9 Nm^2/e^2
                     1 x 10^-7 Ns^2/e^2

                   = 9 x 10^16 m^2/s^2
This is a squared speed due to squared distance over a squared time, therefore the square root must be taken in order to obtain the speed:

                     =3 x 10^8 m/s  or the speed of light

Samuel Morse, the creator of the telegraph, commented on the complexity of the construction of a telegraph wire across the Atlantic Ocean. Such complex tasks compare to the equally complex task of discovering the relationships between all motion, matter, and force, the study of physics.

Lesson 10 Fundamental Forces

The variety of phenomena in the universe can be described by four forces: the strong nuclear force, the weak nuclear force, the electrical force, and the force of gravity. These are the four fundamental forces of nature, and every piece of matter is subject to these forces.

The first two fundamental forces of stong nuclear force and weak nuclear force are located in the nucleous of an atom.

The strong nuclear force is represented by neutrons in the nucleous that overcome the natural repulsion of protons, and bring the protons together. The power released in nuclear reactions is also due to the strong nuclear force. Reactions such as this are present on the sun.

The weak nuclear force has subtle effects in the nucleous and can be represented by the death of stars and the decay of radioactive isotopes. Below is a video that explains the two forces in great detail:



Gravity accelerates mass and reaches out over the bounds of the entire universe. Gravity is explained in terms of force which is measured in newtons.

In 1798, Henry Cavendish weighed the earth and was able to measure the constant in Newton's Law of Universal Gravitation (the force between any two objects):

F = ma                                                  F = mg

F = kg (m/s^2)                                     F = mm(e)
                                                                     r(e)^2

   = N                                                    Gm(e) = gr(e)^2         9.800 m/s^2

                                                             Gm(e) = (9.800 m/s^2) r(e)^2

                                                              r = (6.378 x 10^6 m)^2

                                                              Gm(e) = 3.986 x 10^14 Nm^2/kg

After finding Gm(e), Cavendish was able to weigh the earth using a device depicted below:

In this device, the gravitational force between the two masses causes the bar to twist. By timing the beam's oscillation, Cavendish measured the inertia of the beam with the two balls. The attraction to the other balls could be measured by deflection of the beam and Cavendish found G to be about 6.67 x 10^-11. Cavendish then took Gm(e) and divided it by G to find that the mass of the earth was 5.976 x 10^24 kg.

In regards to the force of electricity, everything is at equilibrium. For example, protons have a positive electrical charge, neutrons have a neutral electrical charge, and electrons have a negative electrical charge. However, all elements are stable with an equal amount of protons and electrons to produce an overall neutral charge.

The force of electricity:

F(e) = k(e) q1q2 r^
                     r^2
where k is the electrical constant, q1 and q2 are the charges, and r^2 is the square of the distance between two objects.

Spring action, friction and viscosity are all electrical forces. A metal spring exhibits electrical force because positively charged metal ions are glued by negatively charged electrons, and as the positive metal ions pull the spring apart, the negatively charged electrons pull the spring back together. Friction is the binding of positive and negative forces as they interact, and viscosity exhibits the interaction of negative and positive forces.

All of the forces mentioned above can be observed in ion and proton accelerators, which are commonly used to study the origns of stars. Friction, gravity, strong nuclear force, weak nuclear force, electricity are all present in the accelerator as the ion passes through a charged gas and looses electrons.

In conclusion, the four fundamental forces have similar theorems, thus, scientists believe there is a single force that explains all. This is known as the Single Unified Theory, however research still continues to this day.

Lesson 9 Moving in Circles

The universe, a contantly expanding void with a plethora of spheres turning on axes. Every planet and satelite in the universe was once believed to orbit in uniform circular motion, a motion that has both constant speed and constant acceleration.

Plato, a student of Socrates, a Greek philosopher, and a mathematician stated that all motions in the heavens must be circular and uniform. This idea fell in the Greek ideal of a perfect or "ideal" universe where all bodies came to rest and had distinct and "perfect" paths of motion. Plato lived from 423 BC to 347 BC, and after this period, astronomers spent 2,000 years trying to prove Plato's findings. Early astronomers used the circular motions of the heavenly bodies to develop Astrology (reading of horoscopes), to predict harvests and growing seasons in Agriculture, and to navigate. Mesopotamians, Hindus, Native Americans, and Native Americans of Peru all tried to explain the circular motions of the planets, and some of their architectural designs followed the circular form. However, at this time, astronomers still believed the Earth was located in the center of the universe. Therefore the Aristotelian model of the universe changed to the Ptolemaic model of the universe. This change was primarily due to the discovery of the epicycle, where the planets did not orbit the earth in circles, but rather, planets orbited in circles that orbited the earth:

Aristotle's Model of the Universe:

Ptolmey's Model of the Universe:

In the field of mathematics, it was discovered that any point on a circle can be found by its Cartesian coordinates because a vector drawn to each point on a circle has the same length:

x/r = theta

y/r = theta

x = rcos(theta)

y = rsin(theta)

With the information above, each heavenly body was to be a point on a circle moving at a constant rate. The angle theta is the angle measure between the inital starting point and time (t). Therefore, [d(theta)/dt] is constant, and equivalent to omega. Thus at any time (t), theta = omega(t). After one revolution, the angle theta is 2(pi). Finally, angular speed is described by 2(pi)/T = omega. The video below displays how circular motion has two components. These components consist of circular motion and vertical motion. The vertical motion is evident when the orbiting green sphere is displayed on its side:

Circular motion is described by the equation:

r = rcos(omega (t))i^ + rsin(omega (t))j^

where both the Cartesian location [rcos(theta)i^ + rsin(theta)j^] and angular motion at any time (t) where [theta = omega(t)] are considered.

With this discovery and application, the Ptolemaic model of the universe was replaced by the Copernican system with the sun at the center of the universe:

This model explained why the planets varied in brightness and why the retrograde motion of the planets was due to the faster motion of planets with smaller orbits, but it still incorrectly portrayed the orbits of the planets in terms of uniform circular motion. Below is a video displaying the apparent retrograde motion of Mars:


Newton's Theory of the Moon proved the Copernican model and that the planets orbited the sun:

The gravity of the earth makes the moon accelerate as F = ma , the moon continues to accelerate all the time but moves at a constant speed. This contradicts the idea of the derivative where acceleration is the rate of change of velocity. Therefore, Newton realized that the velocity of the moon is actually a vector, or the distance the moon would travel if it were not under the force of the gravity of the earth. Thus, velocity is the length an object can accelerate with constant speed as long as it changes direction. This is because the derivative of a vector explains how a vector is changing either by magnitude or direction. In the case of the moon, the acceleration and velocity have constant magnitude but change direction.

The size of the vectors = distance/time
v = 2(pi)r / T

radius [ v = omega(r)]
velocity [a = omega(v)]
acceleration [a = v^2/r]

Therefore, centripital acceleration is the force required to produce constant uniform motion of a body in orbit under the force of gravity. The length of the radius vector determines gravitational force, and this force determines acceleration. This is why planets that are located farther away from the sun take a longer period of time to complete their orbits.

Circular motion requires this relationship between the magnitude of the radius, speed, and acceleration:

a = Gm(e)
          r^2

If a body starts out with just the right velocity, speed is constant and uniform circular motion results:

 a = v^2
        r
a = Gm(e)
        r^2

v^2 = Gm(e)
   r          r^2

v = sqrt(Gm(e)/r)

All in all, the planets veritably orbit the sun in elliptical paths. However, in uniform circular motion, the velocity vector is perpendicular to the radius vector  and the acceleration is inward along the radius. According to Newton's second law, any body that executes uniform circular motion  is being accelerated  by some external force. For a body in orbit, this force is gravity.

Lesson 8 The Apple and the Moon

Isaac Newton's Law of Univeral Gravitation explains why all bodies near the surface of the earth fall with constant acceleration and (in context) why an apple but not the moon falls from the sky.

Early Greek astronomers attempted to explain the motion of the bodies in space through uniform circular motion. Copernicus built upon the Greeks studies and placed the sun, rather than the earth, at the center of the "universe" or solar system. However, Copernicus still followed the idea of a uniform universe. Galileo then studied how bodies act under the influence of earth's gravity on earth. Utilizing all of these discoveries, Kepler developed three laws explaining the planetary motions "outside" of the earth in space:

First Law:

Second Law:

The closer a body is to the sun, the faster it moves and the farther a body is from the sun, the slower it moves.

Third Law:

The larger a body's orbit, the longer period of time it takes for the body to complete a revolution along its orbit.

Here is a video desbribing Kepler's three laws:


From these laws Newton deduced that the reason the planets orbit the sun at a constant rate and path, that the reason all bodies fall at the same rate, and that the reason that the moon orbits the earth were all related. Newton found that every two bits of matter in the universe attract each other and that the force of attraction is proportional to each of their masses. This force of attraction has a concentrated net force in the downward position, corresponding to the masses of the two objects. The force weakens inversely as the square of the distance between the two bodies.

F = -G m1m2 r^
               r^2
Let's consider and apple falling from a tree on earth.

F = -G m(apple)m(earth) r^      
              r^2
r = square of distance from the apple to the center of the earth.

F = m(a)a

m(a)a = -G m(apple)m(earth) r^
                               r^2
a = -Gm(E)
       R(E)^2

Gravity does not depend on the mass of the apple, thus gravity has the same effect on all bodies near earth. The constant force of gravity is evident in this video below when two objects are dropped in a vacuum:


g = -Gm(E)    which is 32ft/sec/sec
        R(E)^2

On the moon, the acceleration may be different but it still relates to the universal gravitational constant. The acceleration of a falling body on the moon is 1/6 the acceleration of a falling body on earth. However, why doesn't the moon fall from the sky like the apple?

If a projectile is thrown fast enough it will orbit the earth. Therefore, just as astronauts are held in orbit of the moon, gravity holds the moon in orbit of the earth. 0g or weightlessness is not the absence of gravity; objects are held in orbit as they "fall for eternity." The rate at which the moon falls is much smaller than the rate at which  the apple falls. In fact, the moon falls slower than the apple by a factor of 3,600. Therefore the moon falls 1/20 of an inch every second:

Moon falls towards earth

a(m) = G M(E) mass of earth
                r^2(m) square distance to earth
g = G M(E) mass of earth
          R^2(E) radius of earth
am/g = GM(E)/r^2(m)
            GM(E)/R^2(E)
am/g = R^2(E)
             r^2(m)
am/g = (R(E))2
              r(m)

Every month the moon travels 2(pi)r(m)

2(pi)r(m) = speed
1month

The Law of Inertia states that the moon wants to fly out of the orbit of the earth in a straight line, however, it is held in by the force of gravity.

The speed of the moon is 40,281 in./sec

Using the Pythagorean theorem with the orbit of the moon:

r(m)^2 + d^2 = (s(m) + r(m))^2

d^2 = [s(m)^2] + 2r(m)s(m)       [s(m)^2] is so small it is ignored.

d^2 = 2r(m)s(m)

d^2 = s(m)
2r(m)

s(m) = 1/20 in. (The rate at which the moon falls towards the earth as it "falls for eternity").



         

 

Lesson 7 Integration

In the Seventeenth Century, the idea of integration was discovered by both Leibniz and Newton. However, Newton took complete credit for this discovery and used it to find the area of curved figures. Newton took the first steps to define calculus as a mechanical calculator of both theory and practice. In ancient time periods, Greeks did not have the luxury of utilizing calculus. Instead, Greeks would perform the method of exhaustion. This method divided curved figures into a plethora of simple polygons in order to find the area of curved figures. In fact, this is how the value of pi was discovered as 3.1415... Kepler was able to discover the area and volume of ninety-two new curved shapes using this method. Below is a polygon that is divided into smaller polygons and a circle divided into smaller polygons by the method of exhaustion:

However, what if the area of the space between the curve y = x^2 for all values [0, t] and the x-axis needed to be found? The area can still be divided into rectangles and added together in order to find the area. Leibniz developed a notation for this process using the sumation symbol, therefore:

         t                                       t

summation [f(x) delta x] = integral [f(x) dx]

         a                                       a

Using integration directly the area from 0 to t can be caculated more efficiently. And once calulated, this area would be equal to the integral of y=x^2 at t subtracted by the integral of y=x^2 at 0.

 Once observed, Integration and Differentiation are inverse processes:

f(x)

            t

integral [f(x) dx]

            0

               t

d integral [f(x) dx]

dt            0

                                                                                                   t

This is the First Fundamental Theorem of Calculus:   d integral [f(x) dx]=f(t)

                                                                                      dt            0

When dealing with area (as displayed above), the area between the curve and the x-axis on the interval [t,a], is equivalent to the expression below:

                      t

A(t) = integral dA dx + A(a)

                      a dx

This is the Second Fundamental Theorem of Calculus. Here is a video describing the use of the Second Fundamental Theorem of Calculus:

Integration is not only used to find areas of curved figures but is also used in mechanics. And identical to derviatives, acceleration, velocity, and displacement are all related by their integrals.