Lesson 5 Vectors

Vectors are certain physical quantities with both direction and magnitude that serve as valuable tools for the United States Coast Guard. The Coast Gaurd uses the process of triangulation and must factor in wind speeds, current speeds, and many other vector represented values when searching for a lost or missing vessel. Below is an example of a vector and how one is indicated in a plane:

Displacement, velocity, and acceleration are all vectors and are represented by bolded symbols:

Displacement: s
Velocity: v
Acceleration: a

The magnitude of a vector is determined by values known as scalars. Time, mass, and magnitude are all scalars and are represented by italicized symbols:

Time: t
Mass: m
Magnitude: A or A

Vectors can be both added and subrtacted:

In the seventeenth century, Fermat and Descartes wrote the opening chapter on coordinate systems by connecting both geometry and algebra. However, all coordinate systems work equally well because the laws of physics work everywhere. And the vector expresses this fact.

The dot product of two vectors always produces a scalar. If the dot product is equal to zero, then the vectors are perpendicular to one another. The dot product is modeled in the image below:

From this, the angle between two vectors and the magnitude of a vector can be found:

Cos (theta) = A.B   gives the angle between two vectors.

                   [A] [B]

[A] = square root ((x^2) + (y^2)) gives the magnitude of the vector.



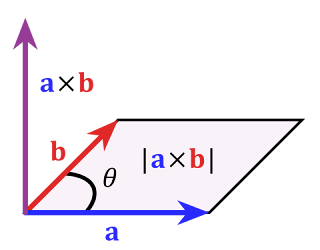
The cross product of two vectors A and B produces the vector AxB. The length or magnitude of AxB is equivalent to the area of the parallelogram formed by the original two vectors A and B:

Direction is determined by the right hand rule:





The right hand rule measures the tendencies of two vectors to be perpendicular. Vectors can also be used as effective tools for describing spinning objects.

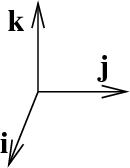
There is a common notation used with vectors such that ^i and ^j are unit vectors <1,1>

^i x ^j = 0

^i x ^i = 1

^j x ^j = 1

<x^i,y^j>

These vectors can also be added, subtracted, multiplied, and divided by one another:

A = Ax^i + Ay^j

B = Bx^i + By^j

A+B = Ax^i + Ay^j + Bx^i + By^j

         = <Ax + Bx>^i + <Ay + By>^j

A . B = <Ax^i + Ay^j> . <Bx^i + By^j>

          = Ax^i . <Bx^i + By^j> + Ay^j . <Bx^i + By^j>

          = AxBx + AyBy

Vectors can also be represented in the three dimensional coordinate plane:

<x^i + y^j + z^k> is equal to the diagonal line drawn from the origin of i j and k in the image above.