Plato, a student of Socrates, a Greek philosopher, and a mathematician stated that all motions in the heavens must be circular and uniform. This idea fell in the Greek ideal of a perfect or "ideal" universe where all bodies came to rest and had distinct and "perfect" paths of motion. Plato lived from 423 BC to 347 BC, and after this period, astronomers spent 2,000 years trying to prove Plato's findings. Early astronomers used the circular motions of the heavenly bodies to develop Astrology (reading of horoscopes), to predict harvests and growing seasons in Agriculture, and to navigate. Mesopotamians, Hindus, Native Americans, and Native Americans of Peru all tried to explain the circular motions of the planets, and some of their architectural designs followed the circular form. However, at this time, astronomers still believed the Earth was located in the center of the universe. Therefore the Aristotelian model of the universe changed to the Ptolemaic model of the universe. This change was primarily due to the discovery of the epicycle, where the planets did not orbit the earth in circles, but rather, planets orbited in circles that orbited the earth:
Aristotle's Model of the Universe:
Ptolmey's Model of the Universe:
In the field of mathematics, it was discovered that any point on a circle can be found by its Cartesian coordinates because a vector drawn to each point on a circle has the same length:
x/r = theta
y/r = theta
x = rcos(theta)
y = rsin(theta)
Circular motion is described by the equation:
r = rcos(omega (t))i^ + rsin(omega (t))j^
where both the Cartesian location [rcos(theta)i^ + rsin(theta)j^] and angular motion at any time (t) where [theta = omega(t)] are considered.
With this discovery and application, the Ptolemaic model of the universe was replaced by the Copernican system with the sun at the center of the universe:
This model explained why the planets varied in brightness and why the retrograde motion of the planets was due to the faster motion of planets with smaller orbits, but it still incorrectly portrayed the orbits of the planets in terms of uniform circular motion. Below is a video displaying the apparent retrograde motion of Mars:
Newton's Theory of the Moon proved the Copernican model and that the planets orbited the sun:
The gravity of the earth makes the moon accelerate as F = ma , the moon continues to accelerate all the time but moves at a constant speed. This contradicts the idea of the derivative where acceleration is the rate of change of velocity. Therefore, Newton realized that the velocity of the moon is actually a vector, or the distance the moon would travel if it were not under the force of the gravity of the earth. Thus, velocity is the length an object can accelerate with constant speed as long as it changes direction. This is because the derivative of a vector explains how a vector is changing either by magnitude or direction. In the case of the moon, the acceleration and velocity have constant magnitude but change direction.
The size of the vectors = distance/time
v = 2(pi)r / T
radius [ v = omega(r)]
velocity [a = omega(v)]
acceleration [a = v^2/r]
Therefore, centripital acceleration is the force required to produce constant uniform motion of a body in orbit under the force of gravity. The length of the radius vector determines gravitational force, and this force determines acceleration. This is why planets that are located farther away from the sun take a longer period of time to complete their orbits.
Circular motion requires this relationship between the magnitude of the radius, speed, and acceleration:
a = Gm(e)
r^2
If a body starts out with just the right velocity, speed is constant and uniform circular motion results:
a = v^2
r
a = Gm(e)
r^2
v^2 = Gm(e)
r r^2
v = sqrt(Gm(e)/r)
All in all, the planets veritably orbit the sun in elliptical paths. However, in uniform circular motion, the velocity vector is perpendicular to the radius vector and the acceleration is inward along the radius. According to Newton's second law, any body that executes uniform circular motion is being accelerated by some external force. For a body in orbit, this force is gravity.



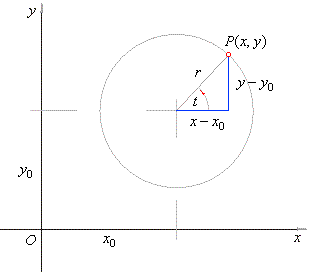

No comments:
Post a Comment